омпьютеры изобрели достаточно давно. В те времена электроникой даже и не пахло. Первые компьютеры были ламповыми и занимали очень много места. Для того, чтобы управлять такой махиной нужно было очень много обслуживающего персонала.

Уже тогда был заложен принцип работы компьютера, который действует до сих пор. А именно, данные передаются с помощью какого-то сигнала (для нас не имеет значения какого, потому что мы не электронщики) методом «есть сигнал или нет» или по-другому «включён или выключен». Так появился «бит» bit. Бит это единица информации, которая может принимать значение или 0, или 1, т.е. «включён или выключен». Восемь бит объединяются в байт, т.е. один байт равен 8 битам. Почему именно 8? Да потому что первые компьютеры были восьми разрядными и могли работать одновременно только с 8-ю битами, например, 010000111.

Немного позже ты узнаешь, что в один байт можно записать любое число до 255. Но это очень мало, поэтому чаще используют более крупные градации:

1.      Два байта = слово.

2.      Два слова = двойное слово.

Итак, компьютер стал работать в двоичной системе исчисления. Но как же тогда записать число 135, если у нас единица информации может быть только или 0 или 1. Просто в двоичной системе. Давай разберёмся, как это работает.

Для начала вспомним, как работает наша десятичная система исчисления, к которой мы привыкли. Для этого рассмотрим число 519578246. Я специально выбрал такое число, чтобы оно состояло из восьми разрядом. Теперь запишем его, как на рисунке ниже:

 

 

Как видишь, я пронумеровал разряды, начиная с нуля до восьми, и справа налево. Теперь представь себе, что это не целое число, а просто набор разрядов. 5, 1, 9, 5, 7, 8, 2, 4 и 6. Как из этих разрядов получить целое число? Наверно некоторые скажут, что надо просто записать их подряд. А если я спрошу, почему? Вот тут появляется математика. Нужно каждый разряд умножить на 10 (степень исчисления) возведённую в степень номера разряда. Непонятно? Попробую оформить в виде формулы:

 

 

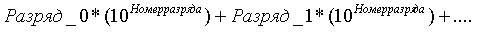
Давай посчитаем по этой формуле, начиная с нулевого разряда. Получается, что 6 нужно умножить на 10 в нулевой степени 6*10⁰=6. Потом прибавить 4*10 в 1 степени 4*10¹= 40 (итого уже 46). Потом 2*10 во второй степени 2*10²=200 (итого 246). Потом 8*10 в 3 степени 8*10³= 8000 (итого 8246) и так далее. В итоге получится число 519578246.

А теперь рассмотрим двоичную систему. Здесь каждый разряд может быть или 0 или 1 (2 состояния). Кстати, в десятичной системе у нас каждый разряд мог быть от 0 до 9, то есть десять состояний. Давай рассмотрим следующий байт - 010000111. Запиши его на листке бумаги так, как показано на рисунке ниже.

Здесь действует та же самая формула, только нужно возводить в степень не 10, а двойку. Опять же произведём расчёт, начиная с нулевого разряда, т.е. справа налево. Получается, что первую 1 мы должны умножить на 2 в нулевой степени (1*2⁰=1). Следующую единицу нужно умножить на 2¹ получается 2 (итого 2+1=3) и т.д. Вот как это будет выглядеть полностью:

 

(1*2⁰)+(1*2¹)+(1*2²)+(0*2³)+(0*2⁴) +(0*2⁵) +(0*2⁶) +(1*2⁷) +(0*2⁸)=135.

 

Вот так, оказывается, выглядит в двоичной системе число 135. Давай теперь научимся пересчитывать числа из десятичной системы в двоичную систему. Для этого нужно число 135 разделить на 2. Получается 67 и остаток 1 (запомним 1). Теперь 67 делим на 2, получается 33 и остаток 1 (теперь две единицы, т.е. 11). Теперь 33 делим на 2, получаем 16 и остаток 1 (теперь три единицы, 111). Теперь 16 делим на 2, получаем 8 и остаток 0 (всего 0111). Теперь 8/2=4 и остаток 0 (00111). 4/2=2 и остаток 0 (000111). Теперь 2/2=1 и остаток 0 (итого 0000111). 1 на два не делится, значит, просто дописываем её 10000111. Получилось первоначальное число.

Вот так происходит преобразование чисел. В двоичную систему исчисления. Таким же образом можно перевести число в любую систему (двоичная, восьмеричная, шестнадцатеричная и т.д). Для более полного закрепления материала я решил привести таблицу, в которой показаны соответствия десятичных чисел двоичным. Попробуй сам перевести пару чисел туда и обратно.

 

Таблица 1. Таблица соответствия десятичных и двоичных чисел

 

В компьютере принято вести расчёт в двоичной или шестнадцатеричной системе. Вторая вошла в обиход, когда компьютеры стали 16-и разрядными.

Шестнадцатеричная система выглядит немного по-другому. Каждый разряд уже содержит не 2 состояния (как в двоичной) или десять (как в десятичной), а шестнадцать. Поэтому один разряд может принимать значения от 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Буква «A» соответствует 10, «В» соответствует 11 и т. д. Например, число 1A в шестнадцатеричной, равно 26 в десятичной. Почему? Да по всё то же формуле. Только здесь нужно возводить 16 в степень номера разряда. «A» - это десять, нужно умножить на 16⁰ = 10. 1 - первый разряд нужно умножить на 16¹ =16. 10+16=26.

 

Десятичное	Двоичное	Шестнадцатеричное
0	0	0
1	1	1
2	10	2
3	11	3
4	100	4
5	101	5
6	110	6
7	111	7
8	1000	8
9	1001	9
10	1010	A
11	1011	B
12	1100	C
13	1101	D
14	1110	E
15	1111	F
16	10000	10
17	10001	11
18	10010	12
19	10011	13
20	10100	14

Таблица 2. Таблица соответствия десятичных, двоичных и шестнадцатеричных чисел

 

На протяжении всей книги мы будем иногда встречаться с шестнадцатеричной системой исчисления (без этого никуда не денешься), поэтому, когда нужно будет показать, что число шестнадцатеричное, я буду ставить перед ним знак решётки #, например, #13. В других языках, например Assembler или C++ принято ставить в конце числа букву h, например, 13h. Но эта книга о Delphi, поэтому я буду писать так, как принято в этой среде разработки, чтобы потом не возникало никаких проблем.

 

Но это всё целые числа. С числами с плавающей точкой совершенно другая история. Если заранее предусмотрено, что число может быть отрицательным, то его длинна сокращается ровно на один бит. Если неотрицательное целое число может быть 8-ми битным, то число со знаком будет 7-и битным. Первый бит будет означать знак. Если первый бит равен 1, то число отрицательное, иначе положительное.

В дробных числах один байт может быть отведён для целой части и один для дробной. Никогда не смешивают целую и дробную часть в одно целое. За счёт этого, дробные числа всегда будут занимать больше памяти, и операции с ними проходят намного дольше.

На первый взгляд перевод чисел очень сложный, но вручную им пользоваться не обязательно. Человек уже давно придумал для себя хорошего помощника - калькулятор. С его помощью без проблем можно перевести число в любую систему.

Запусти встроенный в Windows калькулятор (Пуск -> Программы -> Стандартные -> Калькулятор).Теперь выбери из меню «Вид» пункт «Инженерный». На рисунке ниже показано окно, которое ты должен увидеть:

 

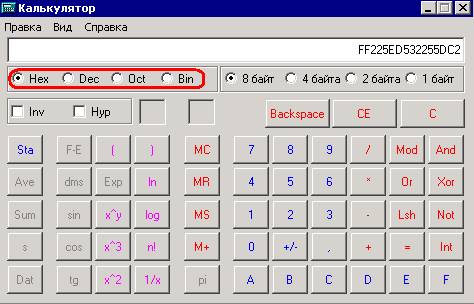
Внешний вид калькулятора

 

Для перевода числа в другую систему, просто набери его и потом выбери нужную систему исчисления. На рисунке я обвёл красным цветом кнопки переключения системы исчисления:

·        Hex - шестнадцатеричная.

·        Dec - десятичная.

·        Oct - восьмеричная.

·        Bin - двоичная.

Возникает вопрос - зачем я тогда так долго рассказывал о преобразованиях, когда так легко воспользоваться калькулятором? Ответ прост - НАДО. Поверь мне. Если ты будешь понимать, как происходит преобразование, то тебе потом легче будет работать с этими числами.

 

Никогда не полагайся только на технику. Всегда полезно знать, как и зачем она что-то делает. Если ты разберёшься с шестнадцатеричным представлением данных, то сможешь простые преобразования делать в уме. Ну а если ты ещё и собираешься стать хакером, то тебе просто необходимо научится хорошо оперировать разными системами исчисления.